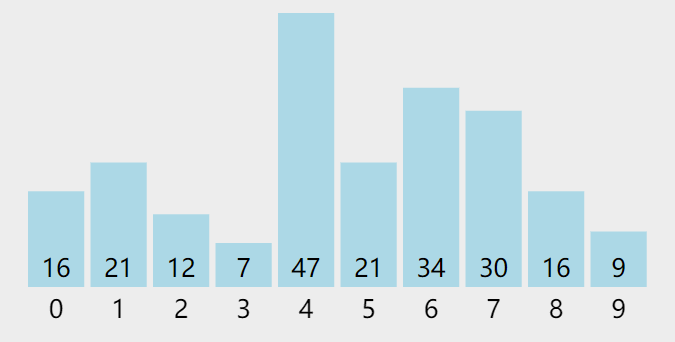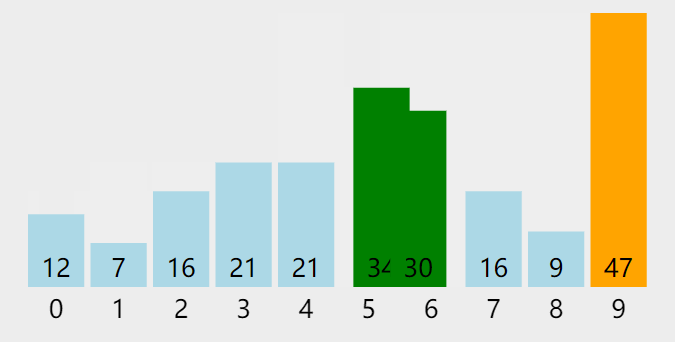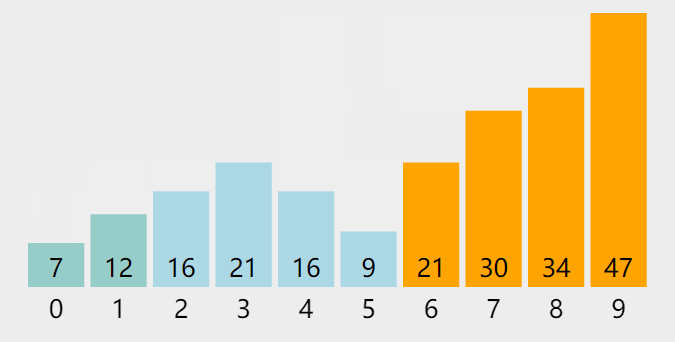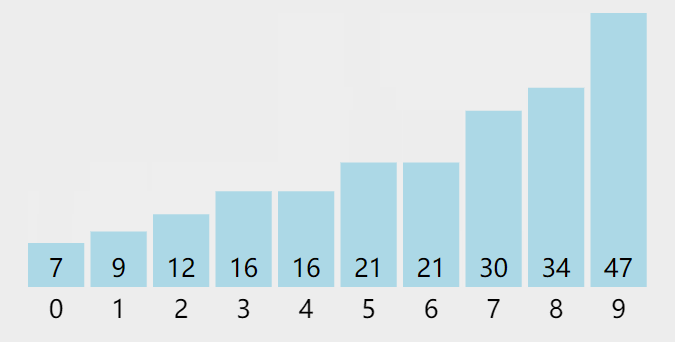
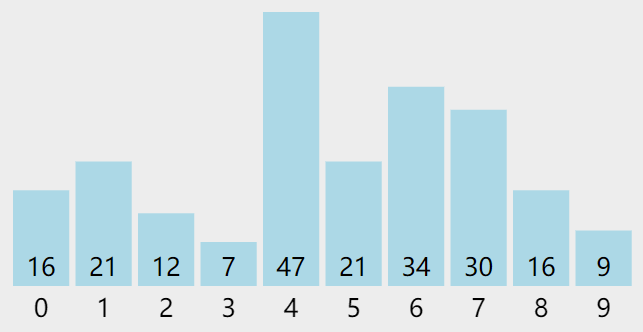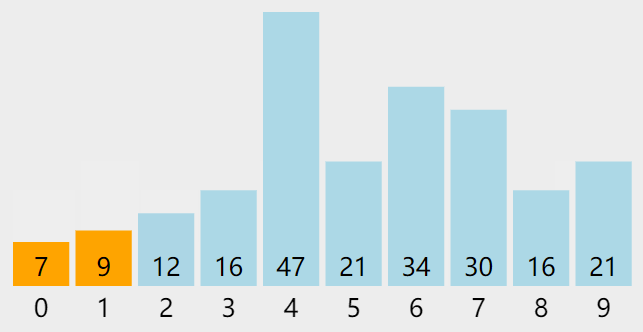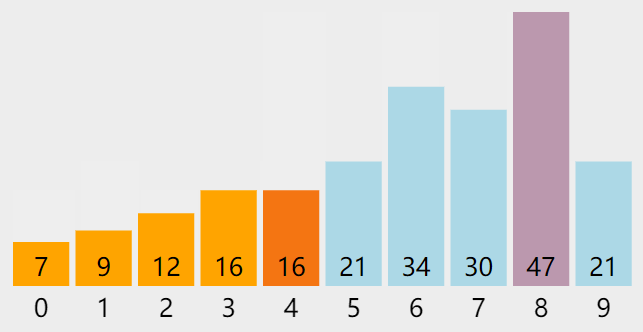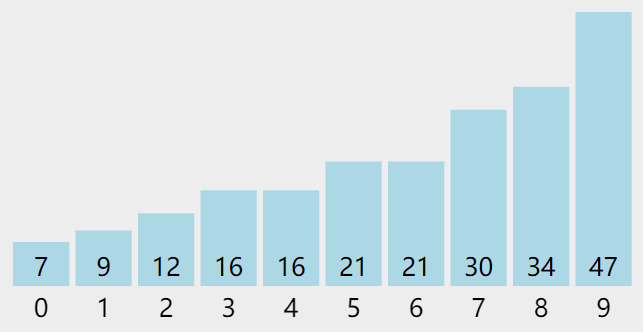算法中常见的排序方法
性能分析
| 算法 | 平均时间复杂度 | 最好情况 | 最差情况 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | $O(n^2)$ | $O(n)$ | $O(n^2)$ | $O(1)$ | 稳定 |
| 快速排序 | $O(n\log n)$ | $O(n\log n)$ | $O(n^2)$ | $O(\log n)$ | 不稳定 |
| 选择排序 | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 不稳定 |
| 堆排序 | $O(n\log n)$ | $O(n\log n)$ | $O(n\log n)$ | $O(1)$ | 不稳定 |
| 插入排序 | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 稳定 |
| 希尔排序 | $O(n^{1.3})$ | $O(n)$ | $O(n^2)$ | $O(1)$ | 不稳定 |
| 归并排序 | $O(n\log n)$ | $O(n\log n)$ | $O(n\log n)$ | $O(n)$ | 稳定 |
| 基数排序 | $O(n\times k)$ | $O(n\times k)$ | $O(n\times k)$ | $O(n+k)$ | 稳定 |
| 桶排序 | $O(n+k)$ | $O(n)$ | $O(n^2)$ | $O(n+k)$ | 稳定 |
- 稳定性:在原序列中,
r[i]==r[j]且r[i]在r[j]之前,而在排序后的序列中r[i]仍在r[j]之前,则称这种排序算法是稳定的
交换排序
冒泡排序(Bubble Sort)
-
性能分析
平均时间复杂度 最好情况 最差情况 空间复杂度 稳定性 $O(n^2)$ $O(n)$ $O(n^2)$ $O(1)$ 稳定 -
排序思路
冒泡排序重复地遍历要排序的列表,一次比较相邻两个元素,如果它们的大小顺序错误则进行交换。
-
排序代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20/**
* 冒泡排序
* @param arr 待排序数组
* @param n 数组长度
*/
public static void bubbleSort(int[] arr, int n) {
// i表示完成排序数字的个数,每一轮排序确认第i+1大的数
for (int i = 0; i < n - 1; i++) {
// 每一轮冒泡排序
// j控制每次比较的元素位置,每轮排序都会把当前最大的数沉底
for (int j = 0; j < n - i - 1; j++) {
// 如果前一个数大于后一个数,则交换它们
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
快速排序(Quick Sort)
-
性能分析
平均时间复杂度 最好情况 最差情况 空间复杂度 稳定性 $O(n\log n)$ $O(n\log n)$ $O(n^2)$ $O(\log n)$ 不稳定 -
排序思路
快速排序是一种常用的排序算法,采用了分治的思想。其基本思路是选择一个基准元素,将小于基准的元素放到基准元素的左边,将大于基准的元素放到基准元素的右边,然后对左右两个子序列分别进行递归排序。
-
排序代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43/**
* 快速排序
* @param arr 待排序数组
* @param left 数组的起始索引
* @param right 数组的结束索引
*/
public static void quickSort(int arr[], int left, int right) {
// 若右边界大于等于左边界,即还存在需要排序的元素
if (right >= left) {
// 选择基准值为左边界元素
int basic = arr[left];
// 定义左右指针
int i = left;
int j = right;
// 循环直到左右指针相遇
while (i < j) {
// 从右向左找到第一个小于基准值的元素
while (i < j && arr[j] > basic) {
j--;
}
// 如果左指针小于右指针,将右指针所指的值赋给左指针,并将左指针右移
if (i < j) {
arr[i] = arr[j];
i++;
}
// 从左向右找到第一个大于基准值的元素
while (i < j && arr[i] < basic) {
i++;
}
// 如果左指针小于右指针,将左指针所指的值赋给右指针,并将右指针左移
if (i < j) {
arr[j] = arr[i];
j--;
}
}
// 将基准值放入指针相遇的位置
arr[i] = basic;
// 递归调用,对基准值左侧的子数组进行排序
quickSort(arr, left, i - 1);
// 递归调用,对基准值右侧的子数组进行排序
quickSort(arr, i + 1, right);
}
}
选择排序
简单选择排序(Selection Sort)
-
性能分析
平均时间复杂度 最好情况 最差情况 空间复杂度 稳定性 $O(n^2)$ $O(n^2)$ $O(n^2)$ $O(1)$ 不稳定 -
排序思路
选择排序每次从待排序的数据元素中选择最小(或最大)的一个元素,放到已排好序的数列的最后(或最前),直到所有元素均排好序。
-
排序代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30/**
* 选择排序
*
* @param array 待排序数组
* @return 排序后的数组
*/
public static int[] selectionSort(int[] array) {
// 如果数组长度为0,直接返回
if (array.length == 0) {
return array;
}
// 外层循环控制每次选择的起始位置
for (int i = 0; i < array.length; i++) {
// 最小索引初始化为i
int minIndex = i;
// 在剩余元素中找到最小值的索引
for (int j = i; j < array.length; j++) {
// 找到最小的数
if (array[j] < array[minIndex]) {
// 将最小数的索引保存
minIndex = j;
}
}
// 交换当前位置i和最小值的位置minIndex的值
int temp = array[minIndex];
array[minIndex] = array[i];
array[i] = temp;
}
return array;
}
堆排序(Heap Sort)
-
性能分析
平均时间复杂度 最好情况 最差情况 空间复杂度 稳定性 $O(n\log n)$ $O(n\log n)$ $O(n\log n)$ $O(1)$ 不稳定 -
排序思路
堆排序利用了堆的数据结构,将待排序的序列构建成一个最大堆(大顶堆或最小堆),然后依次取出堆顶元素(最大值或最小值),并调整剩余元素使之满足堆的性质,最终得到一个有序序列。
-
排序代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61/**
* 堆排序
*
* @param array 待排序数组
* @param n 数组大小
* @return 排序后的数组
*/
public static int[] heapSort(int[] array, int n) {
// 构建最大堆(Max Heap)
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(array, n, i);
}
// 从堆中提取元素,逐步将最大值放到数组末尾
for (int i = n - 1; i >= 0; i--) {
// 将堆顶元素(当前最大值)与数组末尾元素交换
int temp = array[0];
array[0] = array[i];
array[i] = temp;
// 重新构建堆,排除已排序部分
heapify(array, i, 0);
}
return array;
}
/**
* 构建最大堆
*
* @param arr 待构建堆的数组
* @param n 数组大小
* @param i 当前节点索引
*/
public static void heapify(int[] arr, int n, int i) {
// 初始化最大值索引为当前节点索引
int largest = i;
// 左子节点索引
int left = 2 * i + 1;
// 右子节点索引
int right = 2 * i + 2;
// 如果左子节点存在且大于当前节点,则更新最大值索引为左子节点
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// 如果右子节点存在且大于当前节点,则更新最大值索引为右子节点
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// 如果最大值索引不等于当前节点索引,则交换当前节点与最大值节点的值,并继续构建堆
if (largest != i) {
int temp = arr[i];
arr[i] = arr[largest];
arr[largest] = temp;
// 递归调用,对受影响的子树进行堆构建
heapify(arr, n, largest);
}
}
插入排序
直接插入排序(Insertion Sort)
-
性能分析
平均时间复杂度 最好情况 最差情况 空间复杂度 稳定性 $O(n^2)$ $O(n^2)$ $O(n^2)$ $O(1)$ 稳定 -
排序思路
插入排序将待排序的数组分成已排序和未排序两部分,初始时已排序部分只有一个元素(即数组的第一个元素),然后依次将未排序部分的元素插入到已排序部分的适当位置,直到全部元素都被插入到已排序部分,从而得到一个有序数组。
-
排序代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21/**
* 插入排序
*
* @param arr 待排序的整数数组
* @param n 数组长度
*/
public static void insertionSort(int[] arr, int n) {
// 从第二个元素开始遍历数组
for (int i = 1; i < n; i++) {
// 将当前元素插入到已排序部分的适当位置
int key = arr[i];
int j = i - 1;
// 向右移动已排序部分中大于当前元素的元素,为当前元素腾出插入位置
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
// 插入当前元素到适当位置
arr[j + 1] = key;
}
}
希尔排序(Shell Sort)
-
性能分析
平均时间复杂度 最好情况 最差情况 空间复杂度 稳定性 $O(n^{1.3})$ $O(n)$ $O(n^2)$ $O(1)$ 不稳定 -
排序思路
希尔排序是插入排序的一种改进版本,也称为缩小增量排序。它的基本思想是将待排序的数组按照一定的增量分割成若干个子序列,对每个子序列分别进行插入排序,随着增量逐渐减小,每个子序列包含的元素越来越多,当增量减小至1时,整个数组被分成了一个子序列,此时进行的插入排序就是对整个数组的排序。希尔排序的关键在于选择增量序列,常用的增量序列有希尔增量序列、Hibbard增量序列等。
-
排序代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22/**
* 希尔排序
*
* @param arr 待排序的数组
* @param n 数组的长度
*/
public static void shellSort(int[] arr, int n) {
// 初始增量设为数组长度的一半,逐渐减小增量直至1
for (int gap = n / 2; gap > 0; gap /= 2) {
// 对每个子序列进行插入排序
for (int i = gap; i < n; i++) {
int key = arr[i];
int j = i;
// 插入排序的过程,插入的间隔为当前增量gap
while (j >= gap && arr[j - gap] > key) {
arr[j] = arr[j - gap];
j -= gap;
}
arr[j] = key;
}
}
}
更多排序算法
归并排序(Merge Sort)
-
性能分析
平均时间复杂度 最好情况 最差情况 空间复杂度 稳定性 $O(n\log n)$ $O(n\log n)$ $O(n\log n)$ $O(n)$ 稳定 -
排序思路
归并排序将待排序数组分成两个子数组,对每个子数组进行递归地归并排序,然后将已排序的子数组合并成一个有序数组。
-
排序代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79/**
* 归并排序
*
* @param arr 待排序的数组
*/
public static void mergeSort(int[] arr) {
// 调用辅助函数进行归并排序
mergeSort(arr, 0, arr.length - 1);
}
/**
* 辅助函数,对指定范围的数组进行归并排序
*
* @param arr 待排序的数组
* @param left 数组的起始索引
* @param right 数组的结束索引
*/
private static void mergeSort(int[] arr, int left, int right) {
if (left < right) {
// 计算中间位置
int mid = (left + right) / 2;
// 对左半部分进行归并排序
mergeSort(arr, left, mid);
// 对右半部分进行归并排序
mergeSort(arr, mid + 1, right);
// 合并左右两部分
merge(arr, left, mid, right);
}
}
/**
* 辅助函数,合并两个已排序的子数组
*
* @param arr 待排序的数组
* @param left 左子数组的起始索引
* @param mid 左子数组的结束索引
* @param right 右子数组的结束索引
*/
private static void merge(int[] arr, int left, int mid, int right) {
// 计算左右两部分的长度
int n1 = mid - left + 1;
int n2 = right - mid;
// 创建临时数组存放左右两部分的元素
int[] leftPart = new int[n1];
int[] rightPart = new int[n2];
// 将元素拷贝到临时数组中
for (int i = 0; i < n1; ++i) {
leftPart[i] = arr[left + i];
}
for (int j = 0; j < n2; ++j) {
rightPart[j] = arr[mid + 1 + j];
}
// 合并两个子数组
int i = 0, j = 0;
int k = left;
while (i < n1 && j < n2) {
if (leftPart[i] <= rightPart[j]) {
arr[k] = leftPart[i];
i++;
} else {
arr[k] = rightPart[j];
j++;
}
k++;
}
// 将剩余元素拷贝到数组中
while (i < n1) {
arr[k] = leftPart[i];
i++;
k++;
}
while (j < n2) {
arr[k] = rightPart[j];
j++;
k++;
}
}
基数排序(Radix Sort)
-
性能分析
平均时间复杂度 最好情况 最差情况 空间复杂度 稳定性 $O(n\times k)$ $O(n\times k)$ $O(n\times k)$ $O(n+k)$ 稳定 -
排序思路
基数排序按照低位先排序,然后收集;再按照高位排序,然后再次收集;依次类推,直到最高位。
-
排序代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61/**
* 基数排序
*
* @param arr 待排序数组
*/
public static void radixSort(int[] arr) {
// 获取数组中的最大值,用于确定排序的轮数
int max = getMax(arr);
// 对每一位进行计数排序
for (int exp = 1; max / exp > 0; exp *= 10) {
countingSort(arr, exp);
}
}
/**
* 辅助函数,获取数组中的最大值
*
* @param arr 数组
* @return 数组中的最大值
*/
private static int getMax(int[] arr) {
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
return max;
}
/**
* 辅助函数,计数排序
*
* @param arr 待排序数组
* @param exp 当前位数
*/
private static void countingSort(int[] arr, int exp) {
int n = arr.length;
int[] output = new int[n];
int[] count = new int[10];
// 统计每个数字出现的次数
for (int j : arr) {
count[(j / exp) % 10]++;
}
// 将计数数组转换为前缀和数组
for (int i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
// 从后往前遍历原数组,根据计数数组将元素放到正确的位置上
for (int i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
// 将排好序的数组复制回原数组
System.arraycopy(output, 0, arr, 0, n);
}
桶排序(Bucket Sort)
-
性能分析
平均时间复杂度 最好情况 最差情况 空间复杂度 稳定性 $O(n+k)$ $O(n)$ $O(n^2)$ $O(n+k)$ 稳定 -
排序思路
桶排序将待排序数组分割成若干个桶,然后对每个桶中的元素进行排序,最后按照顺序合并每个桶得到有序数组。
-
排序代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44/**
* 桶排序
*
* @param arr 待排序数组
* @param n 数组长度
*/
public static void bucketSort(int[] arr, int n) {
if (arr == null || n <= 1) {
return;
}
// 找到最大值和最小值
int max = arr[0], min = arr[0];
for (int num : arr) {
max = Math.max(max, num);
min = Math.min(min, num);
}
// 计算桶的数量
int bucketNum = (max - min) / n + 1;
ArrayList<ArrayList<Integer>> buckets = new ArrayList<>(bucketNum);
for (int i = 0; i < bucketNum; i++) {
buckets.add(new ArrayList<>());
}
// 将元素分配到桶中
for (int num : arr) {
int index = (num - min) / n;
buckets.get(index).add(num);
}
// 对每个桶中的元素进行排序
for (ArrayList<Integer> bucket : buckets) {
Collections.sort(bucket);
}
// 将各个桶中的元素按照顺序依次取出,组成有序序列
int index = 0;
for (ArrayList<Integer> bucket : buckets) {
for (int num : bucket) {
arr[index++] = num;
}
}
}