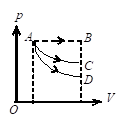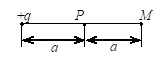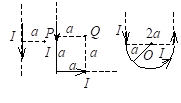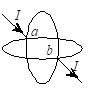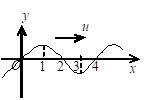大学物理期末复习题
质点力学与运动学
选择题
-
一质点在平面上运动,已知质点位置矢量的表示法为$\vec{r}=at^2\vec{i}+bt^2\vec{j}$(其中a、b为常量),则该质点作(B)
A. 匀速直线运动
B. 变速直线运动
C. 抛物线运动
D. 一般曲线运动
-
质点做曲线运动,$\mathord{ \buildrel{ \lower0pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over r}$标识位置矢量,$\mathord{ \buildrel{ \lower0pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over v}$表示速度,$\mathord{ \buildrel{ \lower0pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over a}$表示加速度,$S$表示路程,$a_t$表示切向加速度,下列表达式中(D)
①$\frac{dv}{dt}=a$
②$\frac{dr}{dt}=v$
③$\frac{dS}{dt}=v$
④$\left | \frac{d\mathord{ \buildrel{ \lower0pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over v}}{d\mathord{ \buildrel{ \lower0pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over t}} \right | =a_t$
A. 只有①、④正确
B. 只有②正确
C. 只有②、④正确
D. 只有③正确
-
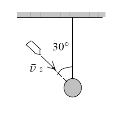
质量为$20g$的子弹,以$400m/s$的速率沿图示方向射入一原来静止的质量为$980g$的摆球中,摆线长度不可伸缩,子弹射入后开始与摆球一起运动的速率为(B)
A. 2m/s
B. 4m/s
C. 7m/s
D. 8m/s
-
一质点在几个外力同时作用下运动时,下述哪种说法正确?(C)
A. 质点的动量改变时,质点的动能一定改变
B. 质点的动能不变时,质点的动量也一定不变
C. 外力的冲量是零,外力的功一定为零
D. 外力的功为零,外力的冲量一定为零
填空题
- (习题1.1)质点x、y、z的分量形式分别为$x=R\cos\omega t,y=R\sin\omega t,z=\frac{h\omega}{2\pi}t$,其中R、h和均为大于零的常量
- 则质点位矢的表达式为:$r=R\cos\omega ti+R\sin\omega tj+\frac{h\omega t}{2\pi}k$
- 任意时刻质点的速度为:$v=-\omega R\sin\omega ti+R\omega\cos \omega tj+\frac{h\omega}{2\pi}k$
- 任意时刻质点的加速度为:$a=-\omega^2R(\cos\omega ti+\sin \omega tj)$
- (习题1.2)已知质点的运动方程为$r=t^2i+(t-1)^2j$(SI单位),则
- 质点的运动轨迹(仅考虑t-1 s>0的情况)为:$\sqrt{y}=\sqrt{x}-1$
- 从t=1s到t=2s质点的位移为:$\Delta r=3i+j$
- t=2s时,质点的速度为:$v_{2s}=4i+2j$
- t=2s时,质点的加速度为:$a_{2s}=2i+2j$
- (习题1.3)一质点做直线运动,其顺时加速度的变化规律为$a=-A\omega^2\cos \omega t$。已知$t=0$时,质点的速度和位移大小分别为$v_0=0$和$x=A$,其中$A$和$\omega$均为大于零的常量,则该质点的运动学方程为:$x=A\cos\omega t$
- (习题1.9)一质量为$m$的质点在$Oxy$平面上运动,其位置矢量为$r=a\cos\omega ti+b\sin\omega tj$,其中$a,b,\omega$都是常量,则质点在任一时刻的加速度为:$a=-a\omega^2\cos\omega ti-b\omega^2\sin\omega tj=-\omega^2r$
判断题
- (思考1.3.1)质点做圆周运动时,加速度一定垂直于速度方向,并指向圆心(✖)
- (思考1.3.2)加速度始终垂直于速度,则质点一定做圆周运动(✖)
- (思考1.3.3)质点在做匀速圆周运动过程中,加速度总是不变(✖)
- (思考1.3.4)只有切向加速度的运动一定是直线运动(✔)
- (思考1.4.1)物体运动方向总和和其所受合外力的方向相同(✖)
- (思考1.4.2)物体一旦受力就会产生加速度(✖)
- (思考1.4.3)物体运动的速率不变,则其所受合外力必然为零(✖)
刚体力学
选择题
-
有两个力作用在一个有固定转轴的刚体上,在以下说法中(B)
①这两个力都平行于轴作用时,它们对轴的合力矩一定是零
②这两个力都垂直于轴作用时,它们对轴的合力矩可能是零
③当这两个力的合力为零时,它们对轴的合力矩也一定是零
④当这两个力对轴的合力矩为零时,它们的合力也一定是零
A. ①②③④都正确
B. ①②正确,③④错误
C. 只有①时正确的
D. ①②③都正确,④错误
-
一轻绳绕在有水平轴的定滑轮上,滑轮的转动惯量为l,绳下端挂一物体。物体所受重力为G,滑轮的角加速度为b,若将物体去掉而以与G相等的力直接向下拉绳子,滑轮的角加速度b将(C)
A. 不变
B. 变小
C. 变大
D. 无法判断
-
一人造地球卫星到地球中心$O$的最大距离和最小距离分别是$R_A$和$R_B$,设卫星对应的角动量分别是$L_A$、$L_B$,动能分别是$E_{KA}$、$E_{KB}$,则应有(D)
A. $L_B>L_A$,$E_{KA}>E_{KB}$
B. $L_B>L_A$,$E_{KA}=E_{KB}$
C. $L_B=L_A$,$E_{KA}=E_{KB}$
D. $L_B=L_A$,$E_{KA}<E_{KB}$
-
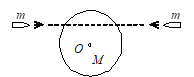
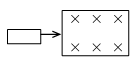
一圆盘正绕垂直于盘面的水平光滑固定轴$O$转动,如图射来两个质量相同,速度大小相同,方向相反并在一条直线上的子弹,子弹射入圆盘并且留在盘内,则子弹射入后的瞬间,圆盘的角速度$\omega$将(C)
A. 增大
B. 不变
C. 减小
D. 不能确定
填空题
- (习题2.1)一个半径为$R=1m$的飞轮以1500转每分钟的转速绕垂直盘面过圆心的定轴转动,受到制动后均匀减速,经$t=50s$后停止。则
- 该飞轮的角加速度为:$a=\frac{\omega-\omega_0}{t}=-\pi rad/s^2$
- 从制动开始到静止转过的圈数为:$N=\frac{\theta}{2\pi}=\frac{\omega_0t+\frac{1}{2}\alpha t^2}{2\pi}=625$
- 制动开始25s时,飞轮的角速度为:$\omega_t=\omega_0+\alpha t=25\pi rad/s$
- (习题2.6)一根质量为$m$,长度为$l$的匀质细杆AB由一摩擦力可略去的铰链悬挂于某处,现欲使细杆恰好能从竖直位置转至水平位置,则需要给细杆的初角速度应该为:$\omega_0=\sqrt{\frac{3g}{l}}$
- (习题2.2)质量为$m$,长度为$l$的均匀细棒AB,其转轴到中心点$O$的距离为$\frac{l}{4}$并与棒垂直,该细棒对于该轴的转动惯量为:$I=\frac{7}{48}ml^2$
- (P57)在跳水比赛中,运动员为了增加在空中的翻腾速度,他采取的方式是将身体收紧,其目的是:减小转动惯量
判断题
- (思考2.1.1)内力矩不会改变刚体对某个定轴的角动量(✔)
- (思考2.1.2)作用力和反作用力对同一轴的力矩之和为零(✔)
- (思考2.1.3)大小相同、方向相反的两个力对同一轴的力矩之和为零(✖)
- (思考2.2.1)作用在定轴转动刚体上的力越大,刚体转动的角加速度越大(✖)
- (思考2.1.4)质量相等、形状和大小不同的刚体,在相同力矩的作用下,它们的角加速度一定相等(✖)
- (思考2.2.2)作用在定轴转动刚体上的合力矩越大,刚体转动的角速度越大(✖)
- (思考2.2.3)作用在定轴转动刚体上的合力矩为零,刚体转动的角速度也为零(✖)
- 作用在定轴转动刚体上的合力矩为零,刚体转动的角加速度也为零(✔)
- (思考2.5)平行于转轴的力对转轴的力矩一定等于零,而垂直与转轴的力对转轴的力矩一定不为零(✖)
气体动理论与热力学
选择题
-
已知一定量的某种理想气体,在温度为$T_1$与$T_2$时分子最概然速率分别为$v_{p1}$和$v_{p2}$,分子速率分布函数的最大值分别为$f(v_{p1})$和$f(v_{p2})$若$T_1>T_2$则(B)
A. $v_{p1}>v_{p2},f(v_{p1})>f(v_{p2})$B. $v_{p1}>v_{p2},f(v_{p1})<f(v_{p2})$
C. $v_{p1}<v_{p2},f(v_{p1})>f(v_{p2})$
D. $v_{p1}<v_{p2},f(v_{p1})<f(v_{p2})$
-
置于容器内的气体,如果气体内各处压强相等,或气体内各处温度相同,则这两种情况下气体的状态(B)
A. 一定都是平衡态
B. 不一定都是平衡态
C. 前者一定是平衡态,后者一定不是平衡态
D. 后者一定时平衡态,前者一定不是平衡态
-
如图所示,一定量理想气体从体积$V_1$,膨胀到体积$V_2$分别经历的过程是:$A\to B$等压过程,$A\to C$等温过程,$A\to D$绝热过程,其中吸热量最多的过程(A)
A. 是$A\to B$
B. 是$A\to C$
C. 是$A\to D$
D. 既是$A\to B$也是$A\to C$, 两过程吸热一样多
-
有两个相同的容器,容积固定不变,一个盛有氨气,另一个盛有氢气(看成刚性分子的理想气体),它们的压强和温度都相等,现将$5J$的热量传给氢气,使氢气温度升高,如果使氨气也升高同样的温度,则应向氨气传递热量是(A)
A. $6J$
B. $5J$
C. $3J$
D. $2J$
-
关于可逆过程和不可逆过程的判断:
①可逆热力学过程一定是准静态过程.
②准静态过程一定是可逆过程.
③不可逆过程就是不能向相反方向进行的过程.
④凡有摩擦的过程,一定是不可逆过程.
以上四种判断,其中正确的是(D)
A. ①②③
B. ①②④
C. ②④
D. ①④
填空题
-
(习题3.1)一定质量的气体在压强保持不变的情况下,温度由$50℃$升高到$100℃$,此时体积变为原来的:$\frac{\delta V}{V_1}=\frac{373}{323}=115.5%$
-
(习题3.3)真空设备内部的压强为$1.013\times 10^{-10}$Pa,若系统温度为$300K$,则此时气体分子数密度为:$n=\frac{p}{kt}=\frac{1.013\times 10^{-10}}{1.38\times 10^{-23}\times 300}m^{-3}\approx 2.45\times10^{10}m^{-3}$
-
(习题4.1)一个打足气的自行车内胎,若在$7.0℃$时轮胎中空气的压强为$4.0\times 10^5$Pa,则在温度变为$37℃$时,轮胎中的空气压强为:$p_0=\frac{T_0}{T}p=\frac{310\times 4.0\times 10^5}{280}Pa\approx 4.43\times10^5Pa$
-
(习题4.3)气缸中贮有$2.0mol$的空气,温度为$27℃$,维持压强不变,而使空气的体积膨胀到原来的3倍,此时空气膨胀时所做的功为:$A=p(V_2-V_1)=2\nu RT_1=9.972\times10^3J$
-
(习题4.4)一定量的空气,吸收了$1.71\times 10^3J$的热量,并保持在$1.0\times 10^5Pa$下膨胀,体积从$1.0\times 10^{-2} m^3$增加到$1.5\times 10^{-2} m^3$,此时空气对外做功为:$A=\int pdV=p(V_2-V_1)=500J$
判断题
-
(思考3.2.1)当容器内部各部分的压强相等时,系统处于平衡态(✖)
-
(思考3.2.2)若容器内各部分的温度相同,则相同处于平衡态(✖)
-
(思考3.2.3)容器内各部分的压强相等,并且容器内各部分分子数密度也相同,则系统处于平衡态(✔)
-
温度和体积均相同的氧气和氮气具有相同的分子平均平动动能(✔)
-
(思考3.7)$1mol$氢气与$1mol$氦气具有相同的内能(✖)
-
(思考4.1)系统含有热量即系统含有功(✖)
-
(思考4.3)系统吸收了热量,其内能必然增加了(✖)
-
系统对外做功其内能必然减少(✖)
-
(思考4.10)绝热压缩气体,其内能一定增加(✔)
-
(思考4.11)系统的温度升高一定是吸收了热量(✖)
-
热量会自动地从高温物体传到低温物体,也可以自动地从低温物体传到高温物体(✖)
静电、电磁、稳恒
简答题
-
(习题5.4)如图所示,在真空中有两个点电荷,$Q_1=+3.0×10^{-8}C$,$Q_2=-3.0×10^{-8}C$,两点电荷相距$0.1$m,若电场中的A点与两点电荷之间等距离且$r=0.1m$时,则A点电场强度的大小为?
点电荷$Q_1$和$Q_2$的电场在A点的场强分别为$E_1$和$E_2$,它们大小相等,合场强$E$在$E_1$和$E_2$的夹角平分线上,平分线与$Q_1Q_2$连线平行,方向向右,合场强$E$的大小为:
$E=E_1\cos 60°+E_2\cos 60°=2E_1\cos 60°=\frac{1}{4\pi\varepsilon_0}\frac{2Q_1}{r^2}\cos 60°=2.7\times 10^4 N/C$
-
(思考6.6)当载流线圈()于磁力线时,磁力矩最小?
垂直
选择题
-
坐标原点放一正电荷$Q$,它在$P$点$(x=+1,y=0)$产生的电场强度为$E$。现在,另外有一个负电荷$-2Q$,试问应将它放在什么位置才能使$P$点的电场强度等于零?(B)
A. x轴上,且x>1
B. x轴上,且-1<x<0
C. y轴上,且y>0
D. yy<0轴上,且x>1
-
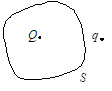
电荷$Q$被曲面$S$所包围 , 从无穷远处引入另一点电荷$q$至曲面外一点,如图所示,则引入前后(D)
A. 曲面S的电场强度通量不变,曲面上各点场强不变
B. 曲面S的电场强度通量变化,曲面上各点场强不变
C. 曲面S的电场强度通量变化,曲面上各点场强变化
D. 曲面S的电场强度通量不变,曲面上各点场强变化
-
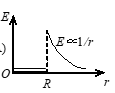
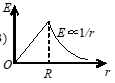
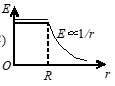
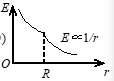
半径为$R$的“无限长”均匀带电圆柱体的静电场中各点的电场强度的大小$E$与距轴线的距离$r$的关系曲线为(B)
A.
B.
C.
D.
-
在点电荷$+q$的电场中,若取图中$P$点处为电势零点 , 则$M$点的电势为(D)
A. $\frac{q}{4\pi \epsilon_0a} $
B. $\frac{q}{8\pi \epsilon_0a} $
C. $\frac{-q}{4\pi \epsilon_0a} $
D. $\frac{-q}{8\pi \epsilon_0a} $
-
半径为$r$的均匀带电球面1,带有电荷$q$,其外有一同心的半径为$R$的均匀带电球面2,带有电荷$Q$,则此两球面之间的电势差$U_1-U_2$为(A)
A. $\frac{q}{4\pi\epsilon_0}(\frac{1}{r}-\frac{1}{R})$
B. $\frac{Q}{4\pi\epsilon_0}(\frac{1}{R}-\frac{1}{r})$
C. $\frac{1}{4\pi\epsilon_0}(\frac{q}{r}-\frac{Q}{R})$
D. $\frac{q}{4\pi\epsilon_0}$
-
一对等量异种电荷同时在同一点射入匀强磁场。已知正、负电荷的速度大小分别为$2v$和$v$,方向都和磁场$B$垂直,则(C)
A. 正电荷先返回到出发点
B. 负电荷先返回到出发点
C. 同时返回到出发点
D. 不知道
-
通有电流I的无限长直导线有如图三种形状,则$P,Q,O$各点磁感强度的大小$B_P,B_Q,B_O$间的关系为(D)
A. $B_P>B_Q>B_O$
B. $B_Q>B_P>B_O$
C. $B_Q>B_O>B_P$
D. $B_O>B_Q>B_P$
-
如图两个半径为R的相同的金属环在$a、b$两点接触(ab连线为环直径),并相互垂直放置。电流$I$沿$ab$连线方向由$a$端流入,$b$端流出,则环中心$O$点的磁感强度的大小为(A)
A. 0
B. $\frac{\mu_0I}{4R} $
C. $\frac{\mu_0I}{R} $
D. $\frac{\sqrt{2}\mu_0I}{R} $
-
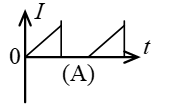
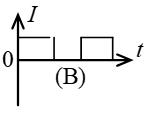
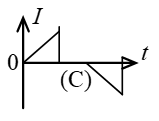
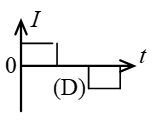
如图所示,一矩形线圈以匀速自无场区平移进入均匀磁场区,又平移穿出。在(A)、(B)、©、(D)各$I-t$曲线中哪一种符合线圈中的电流随时间的变化关系(取逆时针指向为电流正方向,且不计线圈的自感)?(D)
填空题
-
(习题5.1)在氢核(质子)与电子之间的最短距离为$5.3\times 10^{-11}m$,氢核与电子之间的静电力大小为:$F=\frac{1}{4\pi\varepsilon _0}\frac{q_1q_2}{r^2}=8.2\times 10^{-8}N$
-
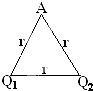
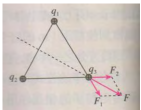
(习题5.2)如图,真空中的三个点电荷,它们固定在边长为50cm的等边三角形的三个定点上,每个电荷的电荷量都是$2\times 10^{-6}C$,每个电荷所受到的静电力大小均为:$F=2F_1\cos 30°=2\times \frac{1}{4\pi\varepsilon_0}\frac{q^2}{r^2}=0.25N$
-
(习题5.5)两个带等量异号电荷的无限大平行平面,电荷的面密度为$\sigma$,则它们之间的电场强度大小为:$E=\frac{\sigma}{2\varepsilon_0}+\frac{\sigma}{2\varepsilon_0}=\frac{\sigma}{\varepsilon_0}$
-
(习题5.10)一根长为L的细棒,被弯成半圆形,其上均匀带电,电荷线密度为$+\lambda$,则圆心处的电势为:$V=\int \mathrm{d}V=\int_{0}^{L} \frac{\lambda \mathrm{d}l}{4\pi\varepsilon_0R}=\frac{\lambda L}{4\pi\varepsilon_0R}=\frac{\lambda} {4\varepsilon_0}$
-
(习题5.13)半径为R的均匀带电球面至于真空中,其电荷面密度为$\sigma$,则球面内的电场强度为:0
-
(思考6.1)在磁感强度为$B$的匀强磁场中,作一个半径为$r$的半球面$S$,$S$的边线所在的平面的法线方向单位矢量$e_n$与$B$之间的夹角为$\alpha$,则通过半球面$S$的磁通量为:$\int\limits_{S}B\cdot\mathrm{d}S=-\pi r^2B\cos \alpha $
-
当电子沿着【垂直】方向射入匀强磁场中,它所受的磁场力最大
-
(思考6.4)若一电子以速度$v$射入磁感应强度为$B$的匀强磁场中,当射入方向【平行】于磁场时,其不受磁场力的作用。
-
(思考6.6)当载流线圈【平行】于磁力线时,磁力矩最大。
-
(思考7.1)感应电动势的大小取决于【磁通量对时间的变化率】
-
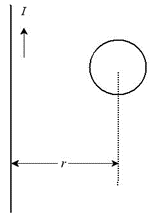
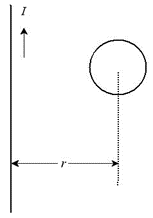
如图所示,当长直导线中的电流逐渐变大时,线圈中的感应电流方向是【逆时针】
-
当导体线圈切割磁力线时,所产生的感应电动势是【动生电动势】
判断题
-
(思考5.1.1)两个完全相同的均匀带电小球分别带电荷量$q_1=2C$(正电荷),$q_2=4C$(负电荷),在真空中相距为r且静止,相互作用的静电力为F。当$q_1,q_2,r$都加倍时,作用力不变(✔)
-
在真空中相距为$r$且静止,相互作用的静电力为$F$,若两个小球的带电量都增加一倍,则它们之间的力也增加一倍(✖)
-
(思考5.7)静电场中的零电势可以随意选择(✔)
-
如果通过一个闭合曲面的电场强度通量为0,那么该曲面上的电场强度处处为零(✖)
-
(思考5.6)在电场中,电场强度为零的点,电势也为零(✖)
-
(思考5.6)在静电场中,电势为零的点电场强度也一定为零(✖)
-
(思考6.7)在匀强磁场中,面积相同、通有相同电流的的线圈,它们的磁矩也相等(✔)
-
(思考7.1)感应电动势的大小取决于磁场强度(✖)
-
感应电荷量与穿过闭合线圈的磁铁速度无关(✖)
-
感应电荷量大小与穿越闭合线圈的磁铁的极性无关(✔)
-
磁场中的洛伦兹力不做功(✔)
-
如图所示,当长直导线中的电流发生变化时,线圈中的感应电动势是感生电动势。 (✔)
简谐振动
简答题
-
(思考8.4)振幅为$A$的弹簧振子,当位移是振幅的一半时,它的势能占总能量的?
势能占总能量的$\frac{1}{4}$
-
(思考8.4)振幅为$A$的弹簧振子,当它的动能和势能相等时,振子的位移是?
位移$x=\frac{\sqrt{2}}{2}A$
-
(习题8.1)一质点按如下规律沿x轴做简谐振动($x=0.05\cos[4\pi(t+\frac{1}{6})]$),则速度的最大值约为?
$v_{max}=A\omega=0.05\times4\pi m/s\approx0.628m/s$
选择题
-
轻质弹簧下挂一个小盘,小盘作简谐振动,平衡位置为原点,位移向下为正,并采用余弦表示。小盘处于最低位置时刻有一个小物体不变盘速地粘在盘上,设新的平衡位置相对原平衡位置向下移动的距离小于原振幅,且以小物体与盘相碰为计时零点,那么以新的平衡位置为原点时,新的位移表示式的初相在(D)
A. $0\sim \frac{p}{2}$之间
B. $\frac{p}{2}\sim p$之间
C. $p\sim \frac{3p}{2}$之间
D. $\frac{3p}{2}\sim 2p$之间
-
一质点沿x轴作简谐振动,振动方程为$x=4\times10^{-2}\cos(2\pi t+\frac{\pi}{3})$。从$t = 0$时刻起,到质点位置在$x=-2 cm$处,且向x轴正方向运动的最短时间间隔为(A)
A. $\frac{1}{2}s$
B. $\frac{1}{4}s$
C. $\frac{1}{6}s$
D. $\frac{1}{8}s$
-
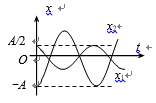
图中所画的是两个简谐振动的振动曲线。若这两个简谐振动可叠加,则合成的余弦振动的初相为(B)
A. $\frac{3}{2}\pi$
B. $\pi$
C. $\frac{1}{2}\pi$
D. 0
-
在下面几种说法中,正确的说法是(C)
A. 波源不动时,波源的振动周期与波动的周期在数值上是不同的.
B. 波源振动的速度与波速相同.
C. 在波传播方向上的任一质点振动相位总是比波源的相位滞后(按差值不大于p计).
D. 在波传播方向上的任一质点的振动相位总是比波源的相位超前.(按差值不大于p计)
-
图示一沿x轴正向传播的平面简谐波在$t=0$时刻的波形.若振动以余弦函数表示,且此题各点振动初相取$-p$到$p$之间的值,则(B)
A. O点的初相为$\phi_0=-\frac{1}{2}\pi$
B. 1点的初相为$\phi_1=0$
C. 2点的初相为$\phi_2=0$
D. 3点的初相为$\phi_3=0$
填空题
- (思考8.2)将弹簧振子的弹簧截去一部分,其振动周期将【减小】
- (思考8.4)振幅为$A$的弹簧振子,当位移是振幅的一半时,它的动能占总能量的:$\frac{3}{4}$
- (习题8.1)一质点按如下规律沿x轴做简谐振动($x=0.05\cos[4\pi(t+\frac{1}{6})]$),则加速度的最大值约为:$a_{max}=A\omega^2\approx7.89m/s^2$
- (习题8.2)设简谐振动的方程为$x=0.02\cos(100\pi t+\frac{\pi}{3})$,则t=1s时相位为:$\frac{301}{3}\pi$
- (习题8.8.3)质量$m=100g$的小球与弹簧构成的系统,按$x=0.05\cos(4\pi t+\frac{\pi}{3})$的规律做自由振动,则振动的能量是:$E=\frac{1}{2}m\omega^2A^2=2\pi^2\times10^{-3}J$
- (习题1.9)一质量为$m$的质点在$Oxy$平面上运动,其位置矢量为$r=a\cos\omega ti+b\sin\omega tj$,其中$a,b,\omega$都是常量,则质点所受的力对原点$O$的力矩为:$M=r\times F=r\times(-m\omega^2r)=-m\omega^2(r\times r)=0$
判断题
- (思考8.1.1)当弹性小球在地面上跳动时,是一种简谐振动。(✖)
- (思考8.1.2)小球在光滑的球形凹槽内进行小幅度摆动时,这是一种简谐振动(✔)
- (思考8.6)阻尼振动也是一种周期性振动(✖)
- (思考8.10.1)同一波线上,相位差为$2\pi$的两个振动质元之间的距离就是在一个周期内振动所传播的距离(✔)
- (思考8.13)机械波可以传递能量,也可以传递动量(✖)