大学物理重要概念及考点参考
重要概念及公式
质点力学与运动学(动量守恒部分)
-
位矢[$r$](矢量):在空间中任选一点参考点,由参考点引向质点所在位置的矢量
-
位移[$\Delta r$](矢量):质点位置变动的大小和方向
-
路程[$S$](标量):质点在其轨迹上经过路径的总长度
-
平均速度[$\bar{v}$](矢量):位置矢量对时间的平均变化率
$\bar{v}=\frac{\Delta r}{\Delta t}$
-
速度/瞬时速度[$v(m/s)$](矢量):位矢对时间的变化率或一阶导数
$v=\lim_{\Delta t \to 0} \frac{\left | \Delta r \right | }{\Delta t}=\left | \frac{\mathrm{d}r}{\mathrm{d}t} \right | $
-
加速度[$\bar{a}(m/s^2)$](矢量):反应速度变化快慢
$\bar{a}=\frac{\Delta v}{\Delta t}$
-
牛顿第一定律:任何物体都保持静止或匀速直线运动状态,直到其他物体所作用的力迫使它改变这种状态为止。
-
牛顿第二定律:物体受到外力作用时,它所获得的加速度的大小与合外力的大小成正比,而与物体的质量成反比;加速度的方向与合外力的方向相同。
$F=ma$
-
牛顿第三定律:作用力与反作用力,大小相等方向相反,$F=-F’$
-
万有引力:物体之间的吸引力(引力常量$G=6.67\times10^{-11}N.m^2/kg^2$,质量$m_1,m_2$,距离$r$,单位矢量$e_r$,由$m_1$指向$m_2$为正)
$F=-G\frac{m_1m_2}{r^2}e_r$
-
重力[$P$](矢量):地球对地面附近物体的万有引力,方向指向地球中心
-
重力加速度[$g$](矢量):重力作用下物体的加速度
$g=\frac{P}{m}$,万有引力定律得到=>$g=G\frac{m_E}{R^2}$(地球质量$m_E$,地球半径$R$)
-
弹性力(矢量):两弹性固体互相接触时施加的作用力
$F=-kx$(弹簧弹性系数$k$,弹簧伸长量$x$)
-
摩擦力[$F_f$](矢量):两个相互接触的物体有相对滑动趋势但还没有相对滑动时产生阻碍相对滑动的力
$F_f=\mu F_N$(动摩擦因数$\mu$,物体正压力$F_N$,方向与相对运动方向相反)
-
功[$A(J)$](标量):
-
恒力沿直线路径做功:$A=F\cos\theta\left | \Delta r\right |=F·\Delta r$
-
变力沿曲线路径做功:质点由a到b过程中每一小段做功之和,$A=\int_{a}^{b}\mathrm{d}A =\int_{a}^{b}F·\mathrm{d}r=\int_{a}^{b}F\cos\theta\left | \mathrm{d}r\right |$
直角坐标系中:$A=\int_{a}^{b}F·\mathrm{d}r=\int_{a}^{b}F_x\mathrm{d}x+F_y\mathrm{d}y+F_z\mathrm{d}z$
-
-
功率[$P(W)$](标量):表示物体做功的快慢
$\bar{P}=\frac{\Delta A}{\Delta t}$,$P=\lim_{\Delta t \to 0}\frac{\Delta A}{\Delta t}=\frac{\mathrm{d}A}{\mathrm{d}t}=F·v$
-
动能[$E_k(J)$](标量):质点运动而具有的能量
$E_k=\frac{1}{2}mv^2$
-
动能定理(牛二导出):F对质点做的功为$A=E_k-E_{k_0}=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2$
-
势能[$E_p(J)$](标量):大小是相对的,与选择的零点有关,等于保守力做功的负值
$\Delta E_p=E_p-E_{p_0}=-A_保$
- 重力势能:$E_p=mgh$
- 弹性势能:$E_p=\frac{1}{2}kx^2$
- 引力势能:$E_p=-G\frac{m_1m_2}{r}$
-
机械能守恒定律:当所有作用于系统的外力对系统所做的功为零且非保守内力所做的功也为零时,系统的机械能恒定不变
-
冲量[$I(N·s)$](矢量):恒力与作用时间的乘积
恒力:$I=F(t-t_0)$
变力:$I=\lim_{\Delta t_i\to0}\sum F_i\Delta t_i=\int_{t_0}^{t}F\mathrm{d}t$
合力:$I=\int_{t_0}^tF\mathrm{d}t=\int_{t_0}^t(\sum_{i=1}^{n}F_i)\mathrm{d}t=\sum_{i=1}^{n}\int_{t_0}^tF_i\mathrm{d}t=\sum_{i=1}^nI_i$(合力在一段作用时间内的冲量等于各分力在同一作用时间内冲量的矢量和,其方向和各分力在同一作用时间内冲量的矢量和的方向相同)
-
动量[$p(kg·m/s)$](矢量):$p=mv$
-
动量定理:作用在质点上的合力$F$在$\mathrm{d}t$时间间隔内的元冲量等于质点动量的增量
$\mathrm{d}p=F\mathrm{d}t$
-
动量守恒定律:在一段时间内作用于质点的合力始终为零时,质点的动量为常矢量
$\int_{t_0}^t(\sum_iF_{i外})\mathrm{d}t=\sum_ip_i-\sum_ip_{i0}=0$
-
力矩[$M(N·m)$](矢量):位置矢量$r$与力$F$的乘积
$M=rFsin\theta$
-
角动量[$L(kg·m^2/s)$](矢量):描述圆周运动物体的运动状态
$L=rmv\sin\theta$
-
角动量定理:作用于质点的合力对参考点的力矩等于质点对该点的角动量随时间的变化率
$M=\frac{\mathrm{d}L}{\mathrm{d}t}$
-
角动量守恒定律:当质点系相对于某一给定参考点的合外力矩为零时,该质点系相对于该给定参考点的角动量矢量保持不变
刚体定轴转动(转动惯量部分)
-
角速度[$\omega(rad/s)$](矢量):$\omega=\lim_{\Delta t\to 0}\frac{\Delta\theta}{\Delta t}=\frac{\mathrm{d}\theta}{\mathrm{d}t}$,方向:右手螺旋定则
-
线速度[$v(m/s)$](标量):$v=\omega r$
-
角加速度[$\alpha(rad/s^2)$](标量):$\omega=\lim_{\Delta t\to 0}\frac{\Delta\omega}{\Delta t}=\frac{\mathrm{d}\omega}{\mathrm{d}t}=\frac{\mathrm{d}^2\theta}{\mathrm{d}t^2}$
-
转动惯量[$I$]:$I=\sum\Delta m_ir_i^2$,积分形式:$I=\int_mr^2\mathrm{d}m$
-
平行轴定理:若两轴平行,其中一轴过质心,则刚体对两轴的转动惯量的关系为$I=I_c+md^2$
-
垂直轴定理:无限小厚度的薄板对一与它垂直的坐标轴的转动惯量,等于薄板对板面内另两直角坐标轴的转动惯量之和。若z轴与薄板垂直,Oxy面在薄板内,则有$I_z=I_x+I_y$
-
组合定理:几个刚体对同一转轴的转动惯量等于各刚体对此转轴的转动惯量之和,即$I=\sum_iI_i$
-
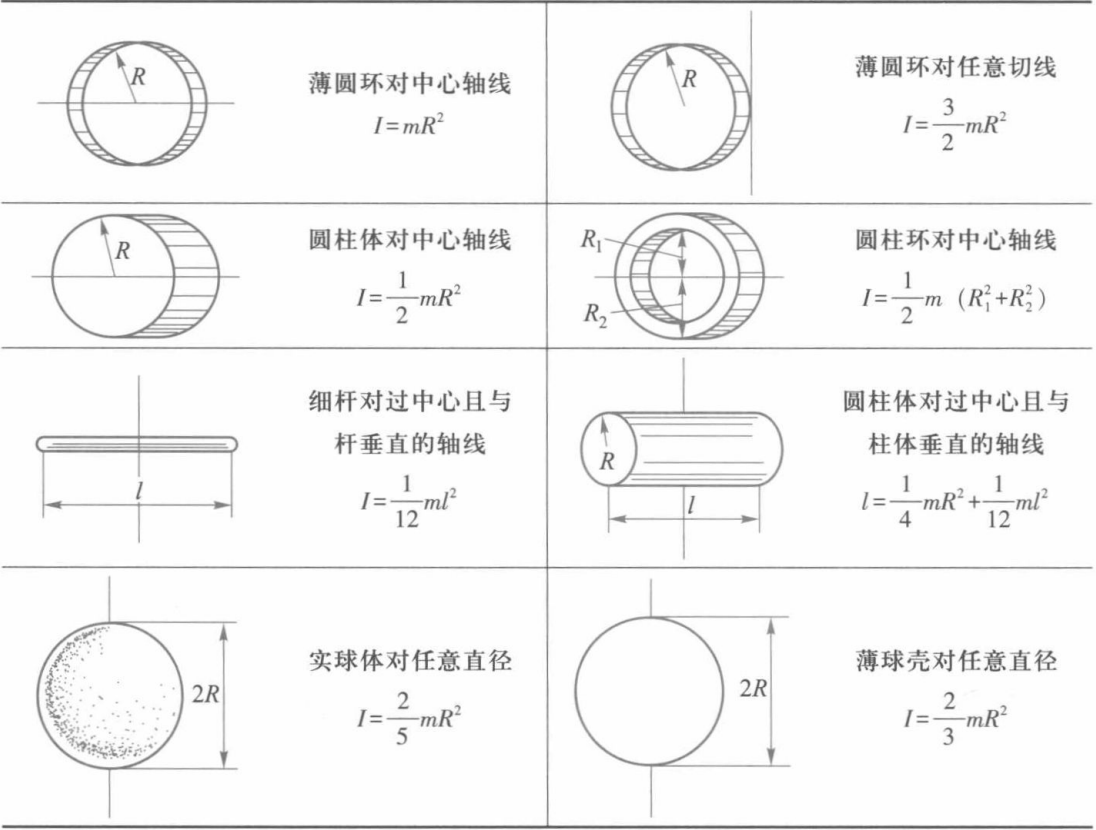
几种常见刚体的转动惯量
静电场
-
元电荷$e\approx1.602\times10^{-19}C$
-
库仑定律:真空中两个静止的点电荷之间的相互作用力的大小与这两个电荷所带电荷量$q_1$和$q_2$的乘积成正比,与它们之间距离$r$的平方成反比, 作用力的方向沿着两个点电荷的连线,同号电荷相斥,异号电荷相吸。
$F_{12}=k\frac{q_1q_2}{r_{12}^2}=\frac{q_1q_2}{4\pi\epsilon_0r_{12}^2}e_{r_{12}}$
-
电场强度[$E(N/C或者V/m)$]:$E=\frac{F}{q_0}$
简谐振动
- 速度[$v$]:$v=-A\omega\sin(\omega t+\varphi)$,$v=\frac{1}{T}=\frac{\omega}{2\pi}$
- 加速度[$a$]:$a=\frac{\mathrm{d}v}{\mathrm{d}t}=-A\omega^2\cos(\omega t+\varphi)=-\omega^2x$
- 振幅[$A$]:$A=\sqrt{x_0^2+\frac{v_0^2}{\omega^2}}$
- 周期[$T$]:$T=\frac{2\pi}{\omega}$,弹簧振子$T=2\pi\sqrt{\frac{m}{k}}$
- 角速度[$\omega$]:$\omega=2\pi v$
- 初相[$\varphi$]:$\varphi=\arctan(-\frac{v_0}{\omega x_0})$
重要考点
动量守恒(1.5.3)
-
例题1.7(P26)
力$F=6ti$(SI单位)作用在$m=3kg$的质点上,质点沿x轴运动,$t=0$时$v_0=0$,求前2s内力F的冲量和力F对m所做的功。
查看解答
由质点动量定理可得,力F的冲量为
$I=\int_0^tF\mathrm{d}t=\int_0^26t\mathrm{d}t=3t^2\Big|_0^2=12N·s$
方向沿x轴正向,因为$I=mv-mv_0=mv$
所以$v=\frac{I}{m}=\frac{12}{3}m/s=4m/s$
浴室由质点的动能定理可得,力F对m所做的功为
$A=E_k-E_{k_0}=\frac{1}{2}mv^2-\frac{1}{2}mv^2_0=\frac{1}{2}mv^2=24J$
-
例题1.8(P26)
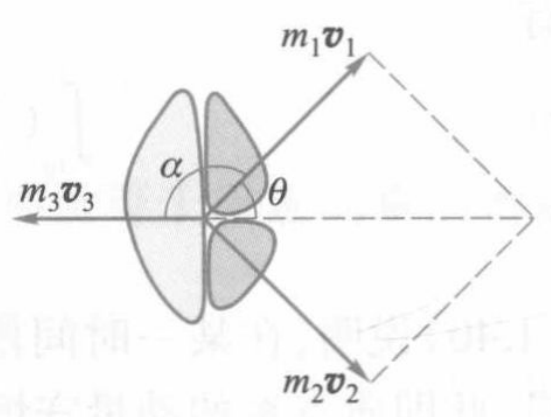
一静止的物体炸裂成三块,其中两块具有相等的质量,且以相同速率$30m/s$沿相互垂直的方向飞开,第三块的质量恰好等于前两块质量之和,求第三块的速度。
查看解答
物体的初动量等于零,炸裂时爆炸力为内力,其远大于重力,所以在爆炸过程中,可以利用动量守恒求其近似解。根据动量守恒定律知道,物体分裂为三块后,这三块碎片的动量总和仍然等于零,即
$m_1v_1+m_2v_2+m_3v_3=0$
因此,这三个动量必处于同一个平面内,且第三块的动量必和第一、二块的合动量大小相等、方向相反。
因为$v_1$和$v_2$相互垂直,所以
$(m_3v_3)^2=(m_1v_1)^2+(m_2v_2)^2$
由于$m_1=m_2=m,m_3=2m$,所以$v_3$的大小为
$v_3=\frac{1}{2}\sqrt{v_1^2+v_2^2}=\frac{1}{2}\sqrt{30^2+30^2}m/s\approx21.2m/s$
$v_3$与$v_1$所成之角$\alpha$由$\alpha=180°-\theta$决定,因为$\tan\theta=\frac{v_2}{v_1}=1,\theta=45°$,所以$\alpha=135°$
即$v_3$与$v_1$及$v_2$都成$135°$角,且三者在同一平面内。
-
例题1.9(P30)
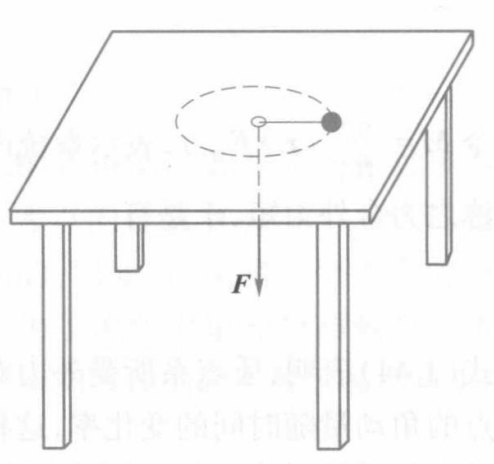
如图所示,水平放置的光滑桌面中间有一光滑小孔,轻绳一端伸入孔中,另一端系一质量为$10g$的小球,小球沿半径为$40cm$的园周做匀速圆周运动,此时从小孔下拉绳的力为$10^{-3}N$。如果继续向下拉绳,并使小球沿半径为$10cm$的园周做匀速圆周运动,那么此时小球的速率为多少?拉力所做的功是多少?
查看解答
以小球为研究对象,根据题意,由于轻绳作用在小球上的力始终通过小孔即圆周运动的中心,为有心力,所以小球受轻绳的拉力大小对小孔的力矩始终为零。因此,在小球整个运动过程中角动量守恒。设小球质量为m,圆周运动半径$r_0=40cm$时其运动速率为$v$,则角动量守恒定律可得
$mv_0r_0=mvr$
又由于轻绳对小球的拉力等于小球圆周运动的向心力,所以有
$F=\frac{mv_0^2}{r_0}$
由以上两式可得
$v_0=\sqrt{\frac{Fr_0}{m}}=\sqrt{\frac{10^{-3}\times 40\times 10^{-2}}{10\times10^{-3}}}m/s=0.2m/s$
$v=\frac{r_0}{r}v_0=\frac{40}{10}\times 0.2m/s=0.8m/s$
再由质点的动能定理可得,轻绳拉力所做的功为
$A=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2=\frac{1}{2}m(v^2-v_0^2)=\frac{1}{2}\times 10\times 10^{-3}\times(0.8^2-0.2^2)J=3.0\times10^{-3}J$
-
例题1.10(P31)
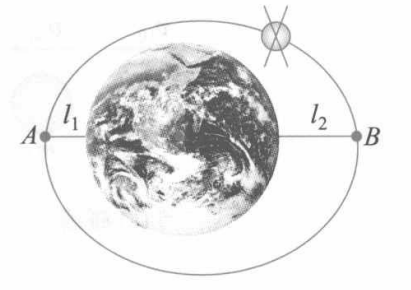
如图所示,我国第一颗人造卫星“东方红”绕地球运行的轨道为一椭圆,地球的中心$O$在椭圆的一个焦点上。已知地球的平均半径为$R=6.371\times10^6m$,卫星在近地点A时,距地面的距离为$l_1=4.39\times10^5$,速率为$v_1=8.1\times10^3m/s$,在远地点B时距离地面的距离$l_2=2.384\times10^6m$,求卫星在远地点B时的速率$v_2$。
查看解答
由于卫星在轨道上运动受地球的引力始终指向地心$O$,引力对地心$O$的力矩为零,所以卫星对地心$O$的角动量守恒
卫星在近地点的角动量为$L_1=mv_1(R+l_1)$
卫星在远地点的角动量为$L_2=mv_2(R+l_2)$
因为角动量守恒,所以$mv_1(R+l_1)=mv_2(R+l_2)$
于是$v_2=v_1\frac{R+l_1}{R+l_2}$
将$R、l_1、l_2、v_1$代入,得
$v_2=v_1\frac{R+l_1}{R+l_2}=\frac{(6.371\times10^6+4.39\times10^5)\times8.1\times10^3}{6.371\times10^+2.384\times10^6}m/s\approx6.30\times10^3m/s$
-
例题1.11(P34)
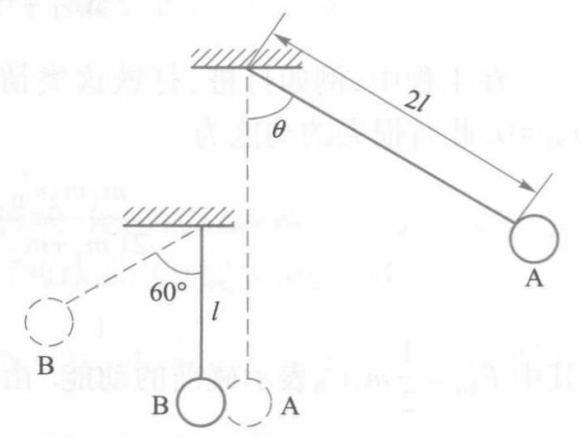
如图所示,两个质量均为m的小球A与B分别悬挂在长度为$2l$和$l$的轻质细绳上,两球碰撞时的恢复系数$e=0.414$。球A与竖直方向的夹角为$\theta$位置处静止释放,下落到竖直方向时与球B正碰,刚好使球B到达与竖直方向的夹角为60°的位置处,那么$\theta$应为多大?
查看解答
以地球为参考系,问题可分解为三个过程:
碰前:球A从$\theta$角位置处静止释放,夏洛到竖直方向还没与球B碰撞的过程。以球A和地球为研究系统,该过程中只有重力做功,系统的机械能守恒。取落至竖直位置时球A的速度大小为$v$,方向水平向左,则由系统的机械能守恒定律得
$\frac{1}{2}mv^2=mg·2l(1-\cos\theta) ······①$
碰时:球A与球B碰撞发生非完全弹性碰撞,可以用动量守恒定律近似求解。设碰后球A与球B的速度大小分别为$v_A、v_B$并水平向左,则由动量守恒定律,得
$mv_A+mv_B=mv······②$
由碰撞定律可得$e=\frac{v_B-v_A}{v}······③$
碰后:球B从竖直方向达到与竖直方向呈60°夹角位置处的过程。以球B和地球为研究系统,该过程中只有重力做功,系统的机械能守恒。取竖直位置时球B所在之处为重力势能零点,则由系统的机械能守恒定律得
$\frac{1}{2}mv_B^2=mg·l(1-\cos60°)······④$
将式①~④联立代入数据得
$\cos\theta=1-\frac{1}{(1-e)^2}=1-\frac{1}{(1+0.414)^2}\approx\frac{1}{2}$
所以$\theta=60°$
转动惯量(2.2.3)
-
例题2.2(P47)
如图所示为质量为$m$,长度为$l$的均匀细棒AB,求该细棒对下两种转轴的转动惯量:
- 转轴通过棒的中心并和棒垂直(a)
- 转轴通过棒的一端并和棒垂直(b)
查看解答
取坐标系如图(a)所示,在棒上距原点$x$处取一长度元$\mathrm{d}x$,设棒的质量线密度为$\lambda$,则该长度元的质量$\mathrm{d}m=\lambda\mathrm{d}x=\frac{m}{l}\mathrm{d}x$。由转动惯量定义,此时棒的转动惯量为
$I_C=\int_{-\frac{l}{2}}^{\frac{l}{2}}x^2\mathrm{d}m=2\int_{0}^{\frac{l}{2}}x^2\frac{m}{l}\mathrm{d}x=\frac{1}{12}ml^2$
当转轴通过棒的一端并和棒垂直时,取坐标系如(b)所示,此时棒的转动惯量为
$I_A=\int_0^lx^2\frac{m}{l}\mathrm{d}x=\frac{1}{3}ml^2$
上述结果表明,同一个物体对于不同的转轴,其转动惯量不同,可见转动惯量与转轴位置有关。由于通过棒的中心并和棒垂直的转轴与通过棒的一端并和棒垂直的转轴之间的垂直距离为$\frac{l}{2}$,应用平行轴定理,有
$I_A=I_C+m(\frac{l}{2})^2=\frac{1}{12}ml^2+\frac{1}{4}ml^2=\frac{1}{3}ml^2$
-
例题2.3(P48)
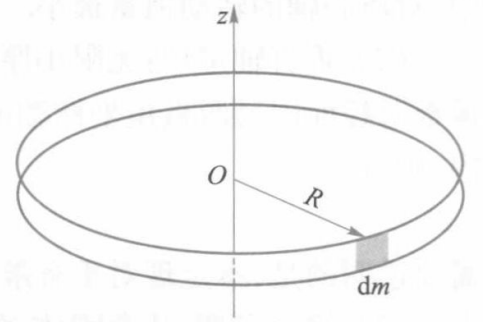
如图所示,求半径为R、质量为m的均匀薄圆环绕垂直环面通过中心转轴的转动惯量。若把圆环改为圆盘,其他条件都不变,试再求之。
查看解答
由于均匀薄圆环中的所有质元都离轴等距离,R为常量。故由转动惯量定义,有
$I=\int r^2\mathrm{d}m=R^2\int \mathrm{d}m=mR^2$
若把圆环改为圆盘,由于圆盘可看成由许多半径不同的同心圆环组成,在圆盘上取一半径为$r$,宽度为$\mathrm{d}r$的圆环,其面积$\mathrm{d}S=2\pi r\mathrm{d}r$,其质量$\mathrm{d}m=\sigma\mathrm{d}S$,其中$\sigma=\frac{m}{\pi R^2}$是圆盘的质量面密度。由此,小圆环对转轴的转动惯量为
$\mathrm{d}I=r^2\mathrm{d}m=r^2\sigma\mathrm{d}S=\frac{2m}{R^2}r^3\mathrm{d}r$
于是整个圆盘对转轴的转动惯量为
$I=\int_mr^2\mathrm{d}m=\frac{2m}{R^2}\int_0^Rr^3\mathrm{d}r=\frac{1}{2}mR^2$
几种常见刚体的转动惯量
简谐振动运动学方程(8.1.2)
-
例题8.1(P238)
一物体沿x轴做简谐振动,平衡位置在坐标原点O,振幅$A=0.06m$,周期$T=2s$,当$t=0$时,物体的位移$x=0.03m$,且向x轴正方向运动。求:
- 此简谐振动的运动学方程
- $t=0.5s$时物体的位移、速度和加速度
查看解答
设该简谐振动的运动学方程为$x=A\cos(\omega t+\varphi)$
则速度为$v=-A\omega\sin(\omega t+\varphi)$
式中,$A=0.06m,\omega=\frac{2\pi}{T}=\pi\mathrm{rad/s}$,将二者与初始条件$t=0$时,$x=0.03m$代入振动的运动学方程得$0.03=0.06\cos\varphi$
解得$\cos\varphi=\frac{1}{2},\varphi=\pm\frac{\pi}{3}$
又因为$t=0$时,物体向x轴正方向运动,即$v=-A\omega\sin\varphi\gt0$
所以初相位应取$\varphi=-\frac{\pi}{3}$
因此该振动的运动学方程为$x=0.06\cos(\pi t-\frac{\pi}{3})$(SI单位)
当$t=0.5s$时,物体的位移为
$x=0.06\cos(0.5\pi-\frac{\pi}{3})\mathrm{m}=0.03\sqrt{3}\mathrm{m}\approx0.052\mathrm{m}$
物体的速度为
$v=-0.06\pi\sin(0.5\pi-\frac{\pi}{3})\mathrm{m/s}=-0.03\pi\mathrm{m/s}\approx-0.094\mathrm{m/s}$
物体的加速度为
$a=-0.06\pi^2\cos(0.5\pi-\frac{\pi}{3})\mathrm{m/s^2}=0.03\sqrt{3}\pi^2\mathrm{m/s^2}\approx-0.51\mathrm{m/s^2}$
-
例题8.2(P241)
质量为0.2kg的物体,以振幅$A=5cm$做简谐振动,其最大加速度$a_{max}=0.2\mathrm{m/s^2}$
- 求振动的周期
- 求通过平衡位置时的动能
- 求总能量
- 物体在何处动能和势能相等
查看解答
因为$a_{max}=A\omega^2$,所以
$\omega=\sqrt{\frac{a_{max}}{A}}=\sqrt{\frac{0.2}{0.05}}\mathrm{rad/s}=2\mathrm{rad/s}$
浴室振动的周期为$T=\frac{2\pi}{\omega}=\frac{2\pi}{2}\mathrm{s}\approx3.14\mathrm{s}$
因为物体通过平衡位置时速度最大,即动能也最大,所以
$E_{k,max}=\frac{1}{2}m\omega^2A^2=\frac{1}{2}\times0.2\times2^2\times0.05^2\mathrm{J}=10^{-3}\mathrm{J}$
总能量为$E=E_{k,max}=10^{-3}\mathrm{J}$
当$E_k=E_p$时,有
$E_k=E_p=\frac{1}{2}E=0.5\times10^{-3}\mathrm{J}$
而$E_p=\frac{1}{2}kx^2=\frac{1}{2}m\omega^2x^2$
故$x=\sqrt{\frac{2E_p}{m\omega^2}}=\sqrt{\frac{2\times0.5\times10^{-3}}{0.2\times2^2}}\mathrm{m}=\frac{\sqrt{2}}{4}\times10^{-1}\mathrm{m}\approx0.035\mathrm{m}$
电偶极子的场强(5.2.1)
例题5.3(P116)
相距为$l$的一对等量异号点电荷系统称为电偶极子。由负电荷指向正电荷的矢量(径矢)作为电偶极子的轴线的正方向,由电荷量$q$与径矢$l$的乘积定义为电偶极矩,简称电距(矢量),用$p$表示,$p=ql$,求真空中电偶极子轴线延长线和中垂线上的场强。

查看解答
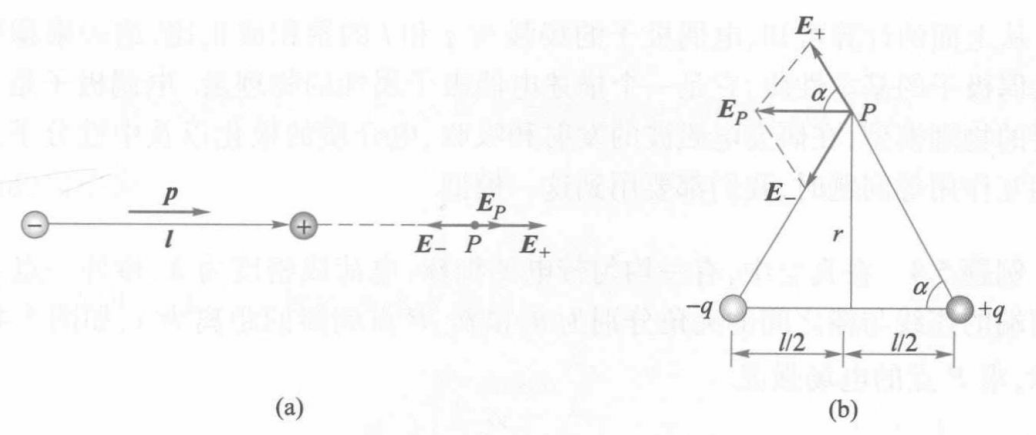
轴线延长线上P点的场强
如图(a)所示,设点电荷$+q$和$-q$轴线的中点到轴线延长线上一点P点的距离为$r(r\gg l)$,$+q$和$-q$在P点产生的场强大小分别为
$E_+=\frac{1}{4\pi\epsilon_0}\frac{q}{(r-\frac{l}{2})^2}$(方向向右)
$E_-=\frac{1}{4\pi\epsilon_0}\frac{q}{(r+\frac{l}{2})^2}$(方向向左)
求$E_+$和$E_-$的矢量和就相当于求代数和,因此P点的合场强$E_P$的大小为
$E_P=E_++E_-=\frac{q}{4\pi\epsilon_0}[\frac{1}{(r-\frac{l}{2})^2}-\frac{1}{(r+\frac{l}{2})^2}]=\frac{1}{4\pi\epsilon_0r^3}\frac{2ql}{(1-\frac{l}{2r})^2(1+\frac{l}{2r})^2}$
因为$r>>l$,所以
$E_P\approx\frac{2ql}{4\pi\epsilon_0r^3}=\frac{2p}{4\pi\epsilon_0r^3}$(方向向右)
写成矢量式为$E_P=\frac{2p}{4\pi\epsilon_0r^3}$
$E_P$的方向与电矩$p$的方向一致。
中垂线上P点的场强
如图(b)所示,设点电荷$+q$和$-q$轴线的中点到中垂线上一点P点的距离为$r(r\gg l)$,$+q$和$-q$在P点产生的场强大小分别为
$E_+=E_-=\frac{1}{4\pi\epsilon_0}\frac{q}{(r^2+\frac{l^2}{4})}$
合场强的大小为
$E_P=2E_+\cos\alpha=2\frac{1}{4\pi\epsilon_0}\frac{q}{(r^2+\frac{l^2}{4})}·\frac{\frac{l}{2}}{(r^2+\frac{l^2}{4})^{\frac{1}{2}}}$
因此,简化为
$E_P=\frac{1}{4\pi\epsilon_0}\frac{ql}{(r^2+\frac{l^2}{4})^{\frac{3}{2}}}$
由于$r\gg l$,所以
$E_P\approx\frac{ql}{4\pi\epsilon_0r^3}=\frac{1}{4\pi\epsilon_0}\frac{p}{r^3}$
$E_P$的方向与电矩的方向相反,故写成矢量式为
$E_P=-\frac{1}{4\pi\epsilon_0}\frac{p}{r^3}$
热力学基础
-
例题3.2
设空气可视为各处温度均为T的理想气体,试求大气压强随高度的变化规律.
查看解答
电磁感应
-
例题7.4
半径为R的圆柱形无限长螺线管中存在均磁场B,而且dB/dt为一大于零的常量,试求螺线管内外感生电场的分布.
查看解答